P: 3,
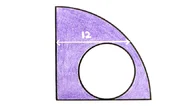
P: 4,
Magmas
P: 8,
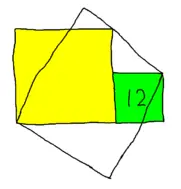
P: 8,

P: 2,
Theory of formal languages
P: 4,
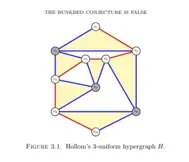
How???
P: 4,

P: 5,

BB(5) = 47,176,870
P: 11,

Random functions
P: 35,

P: 21,
TIL vectors can be scalars
P: 25,

Things math teachers say
P: 8,
puzzle
P: 7,
2024 IB math AA HL P1&P2 problem solving thread
P: 33,
Ternary systems
P: 10,

book shopping
P: 5,

P: 1,
Straightedge constructions
P: 8,

learning math
P: 17,
Recalculation of π and φ
P: 14,

Ted Kaczynski's PhD Thesis
P: 5,

Cubes in a dodecahedron
P: 4,
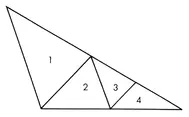
Acute Dissection
P: 3,

Pigeons
P: 3,
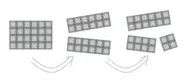
Breaking a Chocolate Bar
P: 2,

funsearch
P: 26,

how ?
P: 21,

P: 8,

P: 3,

P: 3,

P: 24,

Rolling All the Numbers
P: 7,
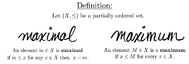
P: 6,

What's your favorite irrational number?
P: 3,
P: 45,

math memes
P: 1,

P: 3,

Lambda-Calculus and Combinators: An Introduction
P: 17,
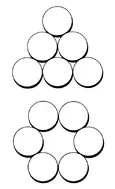
The Sliding Pennies
P: 18,

Homotopy Type Theory
P: 9,
Mathematics is like living in North Korea
P: 5,

Science related boards on altchans
P: 17,

Lean
P: 4,

P: 5,

Sequencing the Digits
P: 18,

P: 1,
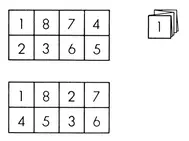
The Folded Sheet
P: 8,

The Flight around the World
P: 9,

P: 2,

Group Russian Roulette
P: 27,

Rings
P: 1,

Division conventions
P: 14,

P: 1,

P: 2,

Axiom of choice
P: 5,

The King's Salary
P: 12,
P: 7,

Conway's Thrackles
P: 26,

Linear Algebra Done Wrong
P: 35,

P: 2,

P: 17,
P: 6,

The SAT will go completely digital next year
P: 12,

P: 3,

Square packing
P: 7,

P: 16,

ET Jaynes' Probability
P: 25,

P: 10,

P: 10,

P: 7,

Math books
P: 2,

P: 18,

The null ritual
P: 1,

covfefe
P: 6,

P: 3,

P: 6,

Supertasks
P: 1,

Steadfast Blinkers
P: 3,

P: 4,

P: 9,

A Poorly Designed Clock
P: 4,

P: 4,
Math question, factoral analysis.
P: 4,

P: 14,
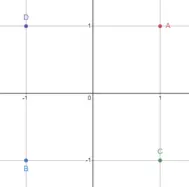
P: 6,

P: 7,

P: 2,

802.11s
P: 8,

P: 5,

P: 4,

P: 12,

The Faulty Combination Lock
P: 4,
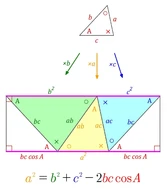
Proofs
P: 37,
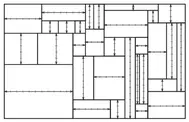
P: 9,

P: 3,

P: 5,
Dividing backwards
P: 4,

P: 13,

Toy Fermat
P: 1,

P: 4,
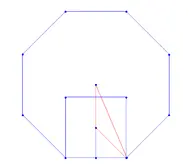
P: 5,

Pick's theorem
P: 5,

P: 7,

Lady Isabel's Casket
P: 1,
what is 0 + 0?
P: 7,

P: 5,

P: 21,

Math problems from everyday life
P: 4,
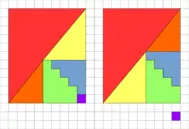
P: 6,

P: 1,

Rubik's cube
P: 43,

P: 4,

P: 1,

P: 11,
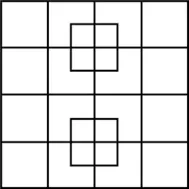
Easiest math puzzle ever
P: 6,
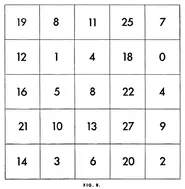
P: 6,
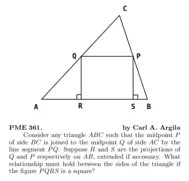
Problem of the day
P: 13,
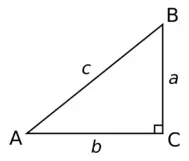
P: 10,

P: 6,
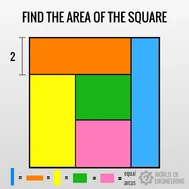
P: 5,
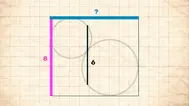
P: 7,
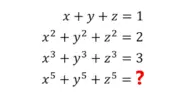
P: 15,

Non-standard analysis and constructive analysis
P: 17,
P: 6,
im a retard help
P: 10,
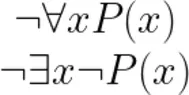
P: 3,
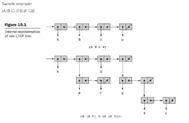
List theory
P: 32,

P: 17,

P: 16,
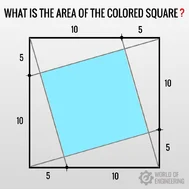
P: 2,
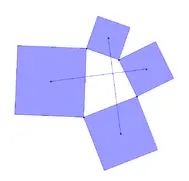
P: 8,
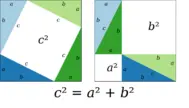
How to prove the Pytha*****an theorem to *****
P: 2,
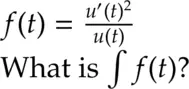
P: 17,

P: 8,
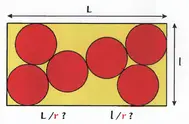
P: 2,

Elementary method to calculate π
P: 3,

P: 8,
In which I keep changing the lisp program from P3661
P: 8,

P: 2,

P: 13,

P: 3,

mandatory thread
P: 6,

P: 9,
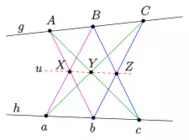
P: 37,
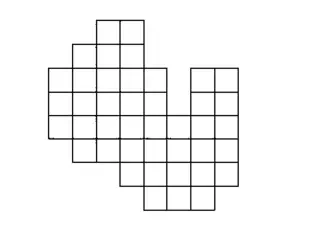
P: 4,

P: 6,
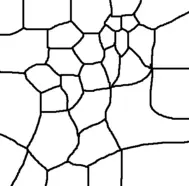
P: 21,

Minimal number of multiplications for 3×3 * 3×3 matrix multiplication.
P: 3,
